Topological Sorting

 

Topological Sorting

  • Difficulty Level : Medium
  • Last Updated : 29 Jan, 2023

Topological sorting for Directed Acyclic Graph (DAG) is a linear ordering of vertices such that for every directed edge u v, vertex u comes before v in the ordering.

Note: Topological Sorting for a graph is not possible if the graph is not a DAG.

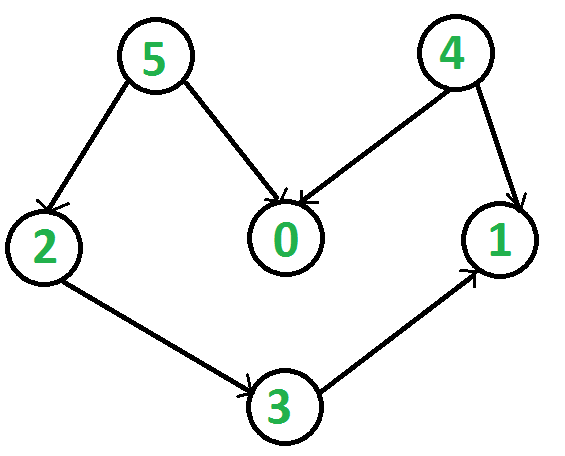
For example, a topological sorting of the following graph is “5 4 2 3 1 0”. There can be more than one topological sorting for a graph. Another topological sorting of the following graph is “4 5 2 3 1 0”. The first vertex in topological sorting is always a vertex with an in-degree of 0 (a vertex with no incoming edges).
 

graph 

Solve Problem
Submission count: 1.2L

Topological Sorting vs Depth First Traversal (DFS): 

In DFS, we print a vertex and then recursively call DFS for its adjacent vertices. In topological sorting, we need to print a vertex before its adjacent vertices. 

For example, in the given graph, the vertex ‘5’ should be printed before vertex ‘0’, but unlike DFS, the vertex ‘4’ should also be printed before vertex ‘0’. So Topological sorting is different from DFS. For example, a DFS of the shown graph is “5 2 3 1 0 4”, but it is not a topological sorting.

Algorithm for Topological Sorting:

Prerequisite: DFS

We can modify DFS to find the Topological Sorting of a graph. In DFS, 

  • We start from a vertex, we first print it, and then 
  • Recursively call DFS for its adjacent vertices. 

In topological sorting,

  • We use a temporary stack. 
  • We don’t print the vertex immediately, 
  • we first recursively call topological sorting for all its adjacent vertices, then push it to a stack. 
  • Finally, print the contents of the stack. 

Note: A vertex is pushed to stack only when all of its adjacent vertices (and their adjacent vertices and so on) are already in the stack

Approach:

  • Create a stack to store the nodes.
  • Initialize visited array of size N to keep the record of visited nodes.
  • Run a loop from 0 till N
    • if the node is not marked True in visited array
      • Call the recursive function for topological sort and perform the following steps.
        • Mark the current node as True in the visited array.
        • Run a loop on all the nodes which has a directed edge to the current node
          • if the node is not marked True in the visited array:
            • Recursively call the topological sort function on the node
        • Push the current node in the stack.
  • Print all the elements in the stack.

Below image is an illustration of the above approach:

Topological-Sorting

Comments

Post a Comment

Popular posts from this blog

Regression and correlation analysis

Image
  Regression and  correlation  analysis Regression analysis involves identifying the relationship between a  dependent variable and one or more  independent variables . A model of the relationship is hypothesized, and estimates of the  parameter  values are used to develop an  estimated regression equation . Various tests are then employed to determine if the model is satisfactory. If the model is deemed satisfactory, the estimated regression equation can be used to predict the value of the dependent variable given values for the independent variables. Regression model In  simple linear regression , the model used to describe the relationship between a single dependent variable  y  and a single independent variable  x  is  y  = β 0  + β 1 x  + ε. β 0  and β 1  are referred to as the  model parameters, and ε is a  probabilistic error term that accounts for the variability in  y  that cannot be explained by the linear relationship with  x . If the  error  term were not present, the model
Read more

Topological data analysis

Image
  Topological data analysis 5 languages Article Talk Read Edit View history From Wikipedia, the free encyclopedia In  applied mathematics ,  topological based data analysis  ( TDA ) is an approach to the analysis of datasets using techniques from  topology . Extraction of information from datasets that are high-dimensional, incomplete and noisy is generally challenging. TDA provides a general framework to analyze such data in a manner that is insensitive to the particular  metric  chosen and provides  dimensionality reduction  and robustness to noise. Beyond this, it inherits  functoriality , a fundamental concept of modern mathematics, from its topological nature, which allows it to adapt to new mathematical tools. [ citation needed ] The initial motivation is to study the shape of data. TDA has combined  algebraic topology  and other tools from pure mathematics to allow mathematically rigorous study of "shape". The main tool is  persistent homology , an adaptation of  homol
Read more

Structure theorem

Image
  Structure theorem [ edit ] The structure theorem is of central importance to TDA; as commented by G. Carlsson, "what makes homology useful as a discriminator between topological spaces is the fact that there is a classification theorem for finitely generated abelian groups." [3]  (see the  fundamental theorem of finitely generated abelian groups ). The main argument used in the proof of the original structure theorem is the standard  structure theorem for finitely generated modules over a principal ideal domain . [9]  However, this argument fails if the indexing set is  ( � , ≤ ) . [3] In general, not every persistence module can be decomposed into intervals. [70]  Many attempts have been made at relaxing the restrictions of the original structure theorem. [ clarification needed ]  The case for pointwise finite-dimensional persistence modules indexed by a locally finite subset of  �  is solved based on the work of Webb. [71]  The most notable result is done by Crawley-Boeve
Read more