Topology
Topology
In mathematics, topology (from the Greek words τόπος, 'place, location' and λόγος, 'study') concerns with the properties of a geometric object that are preserved under continuous deformations, such as stretching, twisting, crumpling, and bending; that is, without closing holes, opening holes, tearing, gluing, or passing through itself.
A topological space is a set endowed with a structure, called a topology, which allows defining continuous deformation of subspaces, and, more generally, all kinds of continuity. Euclidean spaces, and, more generally, metric spaces are examples of a topological space, as any distance or metric defines a topology. The deformations that are considered in topology are homeomorphisms and homotopies. A property that is invariant under such deformations is a topological property. Basic examples of topological properties are: the dimension, which allows distinguishing between a line and a surface; compactness, which allows distinguishing between a line and a circle; connectedness, which allows distinguishing a circle from two non-intersecting circles.
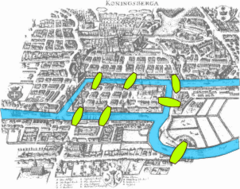
The ideas underlying topology go back to Gottfried Leibniz, who in the 17th century envisioned the geometria situs and analysis situs. Leonhard Euler's Seven Bridges of Königsberg problem and polyhedron formula are arguably the field's first theorems. The term topology was introduced by Johann Benedict Listing in the 19th century, although it was not until the first decades of the 20th century that the idea of a topological space was developed.
Motivation[edit]
The motivating insight behind topology is that some geometric problems depend not on the exact shape of the objects involved, but rather on the way they are put together. For example, the square and the circle have many properties in common: they are both one dimensional objects (from a topological point of view) and both separate the plane into two parts, the part inside and the part outside.
In one of the first papers in topology, Leonhard Euler demonstrated that it was impossible to find a route through the town of Königsberg (now Kaliningrad) that would cross each of its seven bridges exactly once. This result did not depend on the lengths of the bridges or on their distance from one another, but only on connectivity properties: which bridges connect to which islands or riverbanks. This Seven Bridges of Königsberg problem led to the branch of mathematics known as graph theory.
Similarly, the hairy ball theorem of algebraic topology says that "one cannot comb the hair flat on a hairy ball without creating a cowlick." This fact is immediately convincing to most people, even though they might not recognize the more formal statement of the theorem, that there is no nonvanishing continuous tangent vector field on the sphere. As with the Bridges of Königsberg, the result does not depend on the shape of the sphere; it applies to any kind of smooth blob, as long as it has no holes.
To deal with these problems that do not rely on the exact shape of the objects, one must be clear about just what properties these problems do rely on. From this need arises the notion of homeomorphism. The impossibility of crossing each bridge just once applies to any arrangement of bridges homeomorphic to those in Königsberg, and the hairy ball theorem applies to any space homeomorphic to a sphere.
Intuitively, two spaces are homeomorphic if one can be deformed into the other without cutting or gluing. A traditional joke is that a topologist cannot distinguish a coffee mug from a doughnut, since a sufficiently pliable doughnut could be reshaped to a coffee cup by creating a dimple and progressively enlarging it, while shrinking the hole into a handle.[1]
Homeomorphism can be considered the most basic topological equivalence. Another is homotopy equivalence. This is harder to describe without getting technical, but the essential notion is that two objects are homotopy equivalent if they both result from "squishing" some larger object.
History[edit]
Topology, as a well-defined mathematical discipline, originates in the early part of the twentieth century, but some isolated results can be traced back several centuries.[2] Among these are certain questions in geometry investigated by Leonhard Euler. His 1736 paper on the Seven Bridges of Königsberg is regarded as one of the first practical applications of topology.[2] On 14 November 1750, Euler wrote to a friend that he had realized the importance of the edges of a polyhedron. This led to his polyhedron formula, V − E + F = 2 (where V, E, and F respectively indicate the number of vertices, edges, and faces of the polyhedron). Some authorities regard this analysis as the first theorem, signaling the birth of topology.[3]
Further contributions were made by Augustin-Louis Cauchy, Ludwig Schläfli, Johann Benedict Listing, Bernhard Riemann and Enrico Betti.[4] Listing introduced the term "Topologie" in Vorstudien zur Topologie, written in his native German, in 1847, having used the word for ten years in correspondence before its first appearance in print.[5] The English form "topology" was used in 1883 in Listing's obituary in the journal Nature to distinguish "qualitative geometry from the ordinary geometry in which quantitative relations chiefly are treated".[6]
Their work was corrected, consolidated and greatly extended by Henri Poincaré. In 1895, he published his ground-breaking paper on Analysis Situs, which introduced the concepts now known as homotopy and homology, which are now considered part of algebraic topology.[4]
| Manifold | Euler num | Orientability | Betti numbers | Torsion coefficient (1-dim) | ||
|---|---|---|---|---|---|---|
| b0 | b1 | b2 | ||||
| Sphere | 2 | Orientable | 1 | 0 | 1 | none |
| Torus | 0 | Orientable | 1 | 2 | 1 | none |
| 2-holed torus | −2 | Orientable | 1 | 4 | 1 | none |
| g-holed torus (genus g) | 2 − 2g | Orientable | 1 | 2g | 1 | none |
| Projective plane | 1 | Non-orientable | 1 | 0 | 0 | 2 |
| Klein bottle | 0 | Non-orientable | 1 | 1 | 0 | 2 |
| Sphere with c cross-caps (c > 0) | 2 − c | Non-orientable | 1 | c − 1 | 0 | 2 |
| 2-Manifold with g holes and c cross-caps (c > 0) | 2 − (2g + c) | Non-orientable | 1 | (2g + c) − 1 | 0 | 2 |
Unifying the work on function spaces of Georg Cantor, Vito Volterra, Cesare Arzelà, Jacques Hadamard, Giulio Ascoli and others, Maurice Fréchet introduced the metric space in 1906.[7] A metric space is now considered a special case of a general topological space, with any given topological space potentially giving rise to many distinct metric spaces. In 1914, Felix Hausdorff coined the term "topological space" and gave the definition for what is now called a Hausdorff space.[8] Currently, a topological space is a slight generalization of Hausdorff spaces, given in 1922 by Kazimierz Kuratowski.[9]
Modern topology depends strongly on the ideas of set theory, developed by Georg Cantor in the later part of the 19th century. In addition to establishing the basic ideas of set theory, Cantor considered point sets in Euclidean space as part of his study of Fourier series. For further developments, see point-set topology and algebraic topology.
The 2022 Abel Prize was awarded to Dennis Sullivan "for his groundbreaking contributions to topology in its broadest sense, and in particular its algebraic, geometric and dynamical aspects".[10]
Concepts[edit]
Topologies on sets[edit]
The term topology also refers to a specific mathematical idea central to the area of mathematics called topology. Informally, a topology describes how elements of a set relate spatially to each other. The same set can have different topologies. For instance, the real line, the complex plane, and the Cantor set can be thought of as the same set with different topologies.
Formally, let X be a set and let τ be a family of subsets of X. Then τ is called a topology on X if:
- Both the empty set and X are elements of τ.
- Any union of elements of τ is an element of τ.
- Any intersection of finitely many elements of τ is an element of τ.
If τ is a topology on X, then the pair (X, τ) is called a topological space. The notation Xτ may be used to denote a set X endowed with the particular topology τ. By definition, every topology is a π-system.
The members of τ are called open sets in X. A subset of X is said to be closed if its complement is in τ (that is, its complement is open). A subset of X may be open, closed, both (a clopen set), or neither. The empty set and X itself are always both closed and open. An open subset of X which contains a point x is called a neighborhood of x.
Continuous functions and homeomorphisms[edit]
A function or map from one topological space to another is called continuous if the inverse image of any open set is open. If the function maps the real numbers to the real numbers (both spaces with the standard topology), then this definition of continuous is equivalent to the definition of continuous in calculus. If a continuous function is one-to-one and onto, and if the inverse of the function is also continuous, then the function is called a homeomorphism and the domain of the function is said to be homeomorphic to the range. Another way of saying this is that the function has a natural extension to the topology. If two spaces are homeomorphic, they have identical topological properties, and are considered topologically the same. The cube and the sphere are homeomorphic, as are the coffee cup and the doughnut. However, the sphere is not homeomorphic to the doughnut.
Manifolds[edit]
While topological spaces can be extremely varied and exotic, many areas of topology focus on the more familiar class of spaces known as manifolds. A manifold is a topological space that resembles Euclidean space near each point. More precisely, each point of an n-dimensional manifold has a neighborhood that is homeomorphic to the Euclidean space of dimension n. Lines and circles, but not figure eights, are one-dimensional manifolds. Two-dimensional manifolds are also called surfaces, although not all surfaces are manifolds. Examples include the plane, the sphere, and the torus, which can all be realized without self-intersection in three dimensions, and the Klein bottle and real projective plane, which cannot (that is, all their realizations are surfaces that are not manifolds).



Comments
Post a Comment